Função Quadrática ou do 2° Grau

Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0. Vejamos alguns exemplos de funções quadráticas:

• f(x) = 3x2 - 4x  + 1, onde a = 3, b = - 4 e c = 1
• f(x) = x2 -1, onde a = 1, b = 0 e c = -1
• f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
• f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
• f(x) = -4x2, onde a = - 4, b = 0 e c = 0

Gráfico

O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma curva chamada parábola.

Por exemplo, vamos construir o gráfico da função y = x2 + x:

Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.

x	y
-3	6
-2	2
-1	0
0	0
1	2
2	6

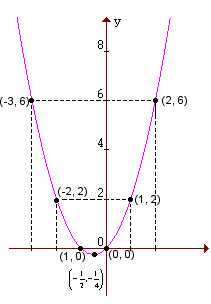
Observação:

Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:

• se   a > 0, a parábola tem a concavidade voltada para cima;
• se   a < 0, a parábola tem a concavidade voltada para baixo;

Uma função é uma regra que liga cada elemento de um conjunto A a um único elemento de um conjunto B, respectivamente conhecidos como domínio e contradomínio da função. Para que a função seja chamada função do segundo grau, é necessário que sua regra (ou lei de formação) possa ser escrita na seguinte forma:

f(x) = ax² + bx + c

ou

y = ax² + bx + c

Além disso, a, b e c devem pertencer ao conjunto dos números reais e a ≠ 0. Dessa forma, são exemplos de função do segundo grau:

a) f(x) = x² + x – 6

b) f(x) = – x²

Raízes da função do segundo grau

As raízes de uma função são os valores assumidos por x quando f(x) = 0. Assim, para encontrá-las, basta substituir f(x) ou y por zero na função e resolver a equação resultante. Para resolver equações do segundo grau, podemos usar fórmula de Bháskara, método de completar quadrados ou qualquer outro método. Lembre-se: como a função é do segundo grau, ela deve ter até duas raízes reais distintas.

Exemplo – As raízes da função f(x) = x² + x – 6 podem ser calculadas da seguinte forma:

f(x) = x² + x – 6
0 = x² + x – 6
a = 1, b = 1 e c = – 6

∆ = b² – 4·a·c
∆ = 1² – 4·1·(– 6)
∆ = 1 + 24
∆ = 25

x = – b ± √∆
      2a
x = – 1 ± √25
      2
x = – 1 ± 5
      2

x’ = – 1 + 5 = 4 = 2
     2        2

x” = – 1 – 5 = – 6 = – 3
  2          2

Logo, as raízes da função f(x) = x² + x – 6 são os pontos de coordenadas A = (2, 0) e B = (– 3, 0).

Vértice da função – Ponto máximo ou mínimo

O vértice é o ponto no qual a função do segundo grau atinge seu valor máximo ou mínimo. Suas coordenadas V = (x_v, y_v) são dadas pelas fórmulas a seguir:

x_v = – b
       2a

e

y_v = – ∆
        4a

No mesmo exemplo citado anteriormente, o vértice da função f(x) = x² + x – 6 é obtido por:

x_v = – b
       2a

x_v = – 1
        2·1

x_v = – 1
       2

x_v = – 0,5

e

y_v = – ∆
       4a

y_v = – 25
        4·1

y_v = – 25
       4

y_v = – 6,25

Assim, as coordenadas do vértice dessa função são V = (– 0,5; – 6,25).

A coordenada y_v também pode ser obtida substituindo o valor de x_v na própria função.

Gráfico da função do segundo grau

O gráfico de uma função do segundo grau sempre será uma parábola. Existem alguns macetes envolvendo essa figura que podem ser usados para facilitar a construção do gráfico. Para exemplificar esses macetes, também usaremos a função f(x) = x² + x – 6.

1 – O sinal do coeficiente a está ligado à concavidade da parábola. Se a > 0 a concavidade da figura será voltada para cima, se a < 0 a concavidade da figura será voltada para baixo.

Assim, no exemplo, como a = 1, que é maior que zero, a concavidade da parábola que representa a função f(x) = x² + x – 6 será voltada para cima.

2 – O coeficiente c é uma das coordenadas do ponto de encontro da parábola com o eixo y. Em outras palavras, a parábola sempre se encontra com o eixo y no ponto C = (0, c).

No exemplo, o ponto C = (0, – 6). Então, a parábola passa por esse ponto.

3 – Assim como no estudo dos sinais da equação do segundo grau, nas funções do segundo grau, o sinal do determinante aponta o número de raízes da função:

Se ∆ > 0 a função tem duas raízes reais distintas.

Se ∆ = 0 a função tem duas raízes reais iguais.

Se ∆ < 0 a função não tem raízes reais.

Dados esses macetes, será preciso encontrar três pontos pertencentes a uma função dosegundo grau para construir o gráfico. Em seguida, basta marcar esses três pontos no plano cartesiano e desenhar a parábola que passa por eles. A saber, os três pontos são:

• O vértice e as raízes da função, se ela possuir raízes reais;

ou

• O vértice e dois outros pontos quaisquer, se a função não possuir raízes reais. Nesse caso, um ponto deve estar à esquerda e outro à direita do vértice da função no plano cartesiano.

Observe que um desses pontos pode ser C = (0, c), exceto no caso em que esse ponto for o próprio vértice.

No exemplo f(x) = x² + x – 6, temos o seguinte gráfico:

SILVA, Luiz Paulo Moreira. "O que é função do segundo grau?"; Brasil Escola. Disponível em <http://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-funcao-segundo-grau.htm>. Acesso em 24 de janeiro de 2018.